리만가설
이건 제타함수라고 부름
리만 가설은 이 함수로부터 시작함
이걸 풀어써보겠음
위에서 아래를 빼자
오른쪽에 2의 배수들이 다 사라졌음!
위에서 아래를 빼자
오른쪽 변에 3의 배수들이 다 없어졌음!
이런식의 반복을 계속 하면...
우변은 1이 되버리고
좌변이 전부 소수들만 나타나 짐 ㄷㄷ
이제
제타함수를 구할수있음!!
따라서
좀 쌈빡한 표현방법
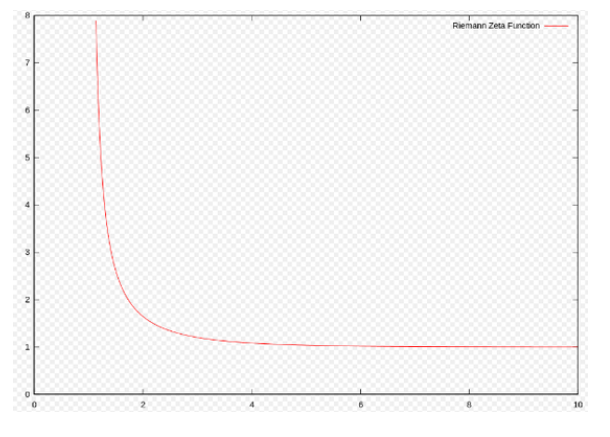
이제 리만은 여기서 그래프가 궁금했음 ㅇㅇ
이제 이 함수의 그래프를 한번 보고싶은것임!!
근데 생각보다 너무 시시했음
리만은 그래서 x의 범위를 복소수로 확장해보았음
근데 복수함수란?
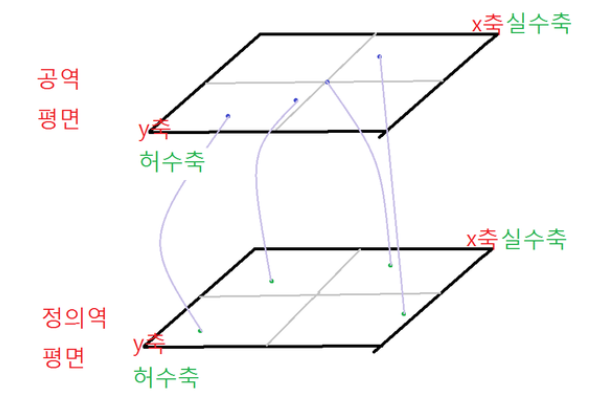
밑에 그림과 같이
복소수는 x+yi . 이렇게 정의역이 (x,y) 두개라서 정의역이 평면이다.
물론 공역도 평면. 그래서 평면에서 평면으로 가는 4차원 함수가 바로 복소함수!
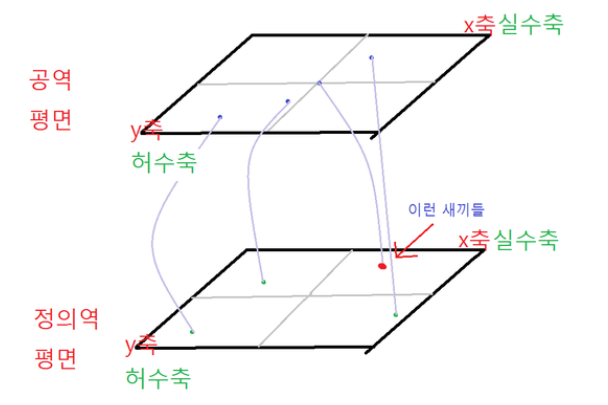
이렇게 정의역을 복소수로 확장한 다음 근이 0이 되는점들은 빨간색으로 찍어봤음
즉
이를테면 이런애들
저렇게 0이 되는 새끼들을 찾았는데 놀라운 현상이 발생!!
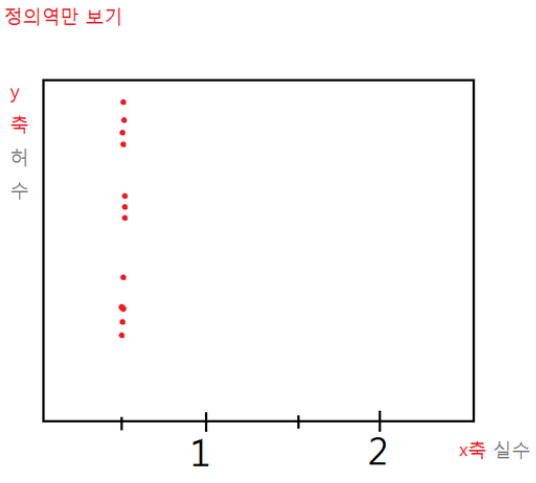
구한 빨간 점들의 실수부가 모조리 1/2 위치에만 찍히는 거임!!!!
여태까지 소수에 관한 특별한 규칙들이 없었는데 이런 규칙을 리만이 발견!
이것이 리만가설
제타함수의 자명하지 않은 모든 근들은
실수부가 1/2 인것 같다.
왜저러는지 증명하면 상금 10억줌
이상임
여까지가 아벨글임..
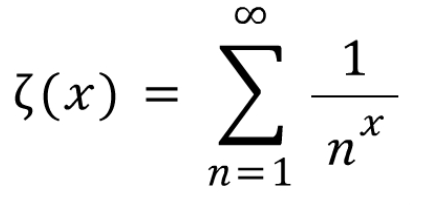
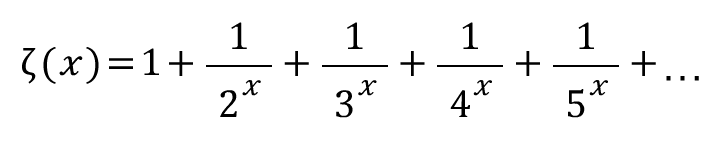
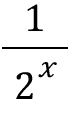
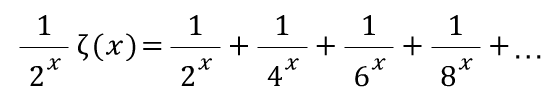
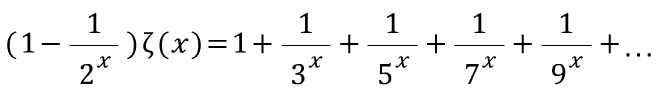
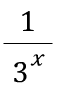
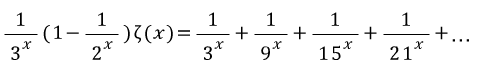
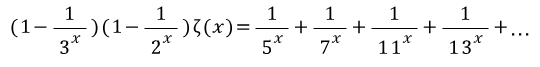
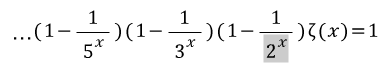
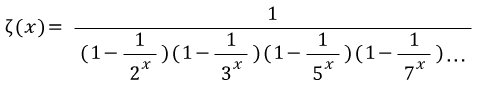
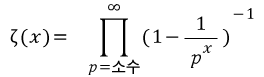

제가 봐도 정말 잘쓴듯 ㄷㄷㄷ 이상임;;
아벨11이 쓴거라고?
아벨이 쓴글 맞고, 리만가설 초보자도 쉽게 이해하게 써서 좋은글인데.. 청일이가 다시 해석해보던가..
ㅇㅘ 아벨 너 어그로아니였음?
요즘 유전이가 리만가설 집중하길래.. 아벨글 올려본것임.
대단하신 형님이네 제가 오해를 했습이다. 용서해주십이요
단순해석인데.. 대단까진 아닌데.. 하여간 설명은 쉽게 잘햇음.. ^^
리만가설의 답을 적어야 대단하다 하겟음.. 이글 올린것중 이유 하나는 업데이트 하란 이야기임..
120 청일아 예의 안 지키면 짤린다.. ^^
레드용님 님이 작성한것도 아니고 아벨이 적은건데(단순해석인데.. 대단까진 아닌데.. 하여간 설명은 쉽게 잘햇음.. ^^)이 댓글이 오해의 소지가 있어요^^ - dc App
뭐 위의 이야기중 모자란부분은 보이지만 초보자들이 쉽게 리만가설을 이해할것 같아서 올렸어요. 모자른부분은 아벨이 채우겠죠.
레드용님 말귀를 못알아먹으시네요 님 실력에 누가 누굴 판단하나용? - dc App
제가 판단하겠죠. ^^ 님이 판단하시나요? ㅎㅎㅎ
근데 드용님 나 작년말부터 갤질했는데 아벨 맨날 똥글만 쌌음. 아벨 원래 저런 컨셉임?
211.36 논문이나 교수 자격증이라도 보여주시면 감사하겠습니다.
내가 생각하는 아벨은 그냥 이것 저것 잡학이 능함.. 철학 수학 물리등등. 그중 의뜸은 인성 같아 보이는데.. 한번은 다중이하다 걸린적 있지만 지금은 안 하는것 같음. 그러나 사람은 좋아보임.. 사회에서 만났다면 좋은 친구였을것 같음.
곡선을 직사각형으로 분할하는분이 리만가설이라니!! - dc App
공부를 잘한다고해서 사람을 잘 가르치란법은 없음.. 어떤 눈높이에 맞추고 어디에 집중을 한다는것이 좋은 교육일것 같다는 생각임.
211.36 곡선이라 말한 링크 가져오렴.. ^^
원이라 말한적은 있어도 곡선이라 말한적은 없는것 같은데..
여러분들 감사합이다!!
211.36 논문이나 교수 자격증 없으면, 뭐 할말 다 한것 아닌가.. ^^
아벨 화이팅~! 업그레이드 부탁함.. 글 깔끔 내가 줄 단위로 정리해서 올린것임.
없는데 니도 없잖아? - dc App
211.36 너가주장하는 내가 곡선이라 말한 링크 찾아오고 이야기해.. 그리고, 매너 없으면 너글도 짤린다.
211.36 또 지금에는 나랑 같다는 이야기 같은데.. 그것은 너 혼자 상상이고, 상상은 꿈에서나 해라. 사이비라 불려도 난 너랑 동급이 되기 싫단다. ^^
요즘 공부를 안해서;; 노력해보겟읍니다
^_________________________^
ㅉ - dc App
ㅆㅅㅌㅊ